Makalah Lingkaran
KATA PENGANTAR
Assalamualaikum, wr.wb
Puji syukur penulis panjatkan ke hadirat Allah SWT, yang telah melimpahkan rahmat dan hidayah-Nya, sehinga penulis dapat menyelesaikan makalah berjudul ”Pembelajaran Matematika SMA Pokok Bahasan Lingkaran” sebagai tugas mata kuliah Pembelajaran Matematika SMA.
Dalam penyusunan makalah ini, penulis mendapat dukungan dari berbagai pihak. Oleh karena itu, penulis mengucapkan terima kasih kepada:
1. Bapak Ariyanto, Drs., M.Pd., selaku dosen mata kuliah Pembelajaran Matematika SMA yang selalu memberikan ilmunya dalam penyelesaian makalah ini
2. Orang tua penulis yang telah membantu baik moril maupun materi
3. Rekan-rekan kelas E yang selalu mendukung dan membantu dalam penyusunan makalah ini
Penulis menyadari bahwa dalam penyusunan makalah ini jauh dari sempurna, baik dari segi penyusunan, bahasan, ataupun penulisannya. Oleh karena itu, penulis mengharapkan kritik dan saran yang sifatnya membangun demi penyempurnaan makalah ini. Akhir kata, semoga makalah ini dapat bermanfaat.
Wassalamualaikum, wr.wb
Surakarta, 11 Maret 2016
Penulis
DAFTAR ISI
HALAMAN JUDUL......................................................................................... i
KATA PENGANTAR...................................................................................... ii
DAFTAR ISI...................................................................................................... iii
BAB I PENDAHULUAN
A. Latar Belakang Masalah.......................................................................... 1
B. Rumusan Masalah.................................................................................... 2
C. Tujuan...................................................................................................... 2
BAB II PEMBAHASAN
A. Definisi Lingkaran................................................................................... 3
B. Jarak Antara Dua Titik............................................................................. 4
C. Persamaan Lingkaran dengan Pusat O(0,0) dan jari–jari r...................... 5
D. Persamaan Lingkaran dengan Pusat M(a,b) dan jari–jari r...................... 6
E. Bentuk Umum Persamaan Lingkaran...................................................... 8
F. Kedudukan Titik Terhadap Lingkaran.................................................... 10
G. Kedudukan Garis Terhadap Lingkaran................................................... 11
H. Jarak Titik Pada Lingkaran...................................................................... 12
BAB III PENUTUP
A. Kesimpulan.............................................................................................. 14
B. Saran........................................................................................................ 14
KUMPULAN-KUMPULAN SOAL............................................................... 15
PEMBAHASAN KUMPULAN-KUMPULAN SOAL................................. 16
DAFTAR PUSTAKA....................................................................................... 22
BAB I
PENDAHULUAN
A. Latar Belakang Masalah
Geometri merupakan salah satu cabang matematika yang sangat penting sebagai ilmu dasar dan sudah dikenal anak-anak sejak kecil. Geometri telah dipelajari pada jenjang pendidikan dasar, pendidikan sekolah menengah, sampai pendidikan tinggi.
Geometri didefinisikan sebagai cabang matematika yang mempelajari tentang titik, garis, bidang, dan benda-benda ruang serta sifat-sifatnya, ukuran-ukurannya, dan hubungannya satu sma lain.
Berdasarkan uraian di atas dalam makalah ini akan di kemukakan tentang materi matematika (geometri) khususnya materi Lingkaran. Pada jenjang pendidikan dasar (sekolah dasar) materi tentang lingkaran hanya sebatas pengenalan bentuk dan unsur-unsurnya, contohnya mudah ditemukan dalam kehidupan sehari-sehari. Selanjutnya meteri lingkaran di tingkat SMP sudah berada pada tingkatan yang lebih tinggi misalnya definisi lingkaran, garis singgung, bagian-bagian lingkaran dan sebagainya. Sedangkan materi lingkaran pada jenjang pendidikan menengah seperti di SMA disajikan dalam bentuk persamaan, seperti persamaan lingkaran, persamaan garis singgung, hubungan bangun ruang dengan lingkaran dan sebagainya.
Dengan demikian materi geometri tentang bangun datar yaitu lingkaran terdapat disetiap jenjang pendidikan mulai dari pendidikan dasar, pendidikan menengah sampai pada pendidikan tinggi dan merupakan dasar untuk setiap jenjang yang lebih tinggi baik pemahaman konsep lingkaran maupun penggunaan lingkaran dalam pemecahan masalah matematika, dalam makalah ini sedikit akan disampaikan materi lingkaran khususnya untuk pendidikan menengah atas.
B. Rumusan Masalah
1. Apa definisi dari lingkaran ?
2. Bagaimana jarak antara dua titik ?
3. Bagaimana persamaan lingkaran dengan pusat O(0,0) dan jari–jari r ?
4. Bagaimana persamaan lingkaran dengan pusat M(a,b) dan jari–jari r ?
5. Bagaimana bentuk umum persamaan lingkaran ?
6. Bagaimana menentukan kedudukan titik terhadap lingkaran ?
7. Bagaimana menentukan kedudukan garis terhadap lingkaran ?
8. Bagaimana menentukan jarak titik pada lingkaran ?
C. Tujuan
1. Untuk mengetahui definisi dari lingkaran
2. Untuk mengetahui jarak antara dua titik
3. Untuk mengetahui persamaan lingkaran dengan pusat O(0,0) dan jari–jari r
4. Untuk mengetahui persamaan lingkaran dengan pusat M(a,b) dan jari–jari r
5. Untuk mengetahui bentuk umum persamaan lingkaran
6. Untuk menentukan kedudukan titik terhadap lingkaran
7. Untuk menentukan kedudukan garis terhadap garis
8. Untuk menentukan jarak titik pada lingkaran
BAB II
PEMBAHASAN
A. Definisi Lingkaran
Perhatikan gambar lingkaran di atas !
Sebuah lingkaran mempunyai beberapa unsur, diantaranya jari – jari dan pusat lingkaran.
O merupakan titik pusat.
OA, OB , dan OC adalah jari – jari .
Jari – jari (r) pada lingkaran memiliki panjang yang sama. Sehingga, OA = OB = OC.
Lingkaran adalah tempat kedudukan titik – titik (himpunan titik) yang jaraknya terhadap satu titik tertentu adalah sama ( konstan ). Titik tertentu disebut pusat lingkaran,dan jarak konstan disebut jari – jari lingkaran.
B. Jarak Antara Dua Titik
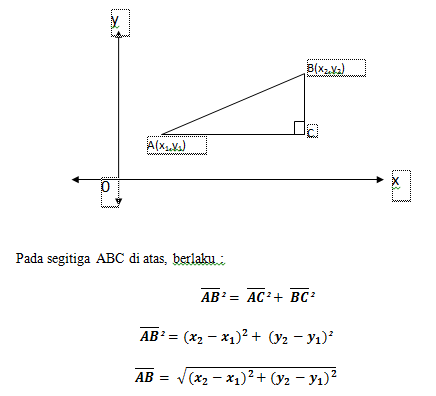
Sebelum memasuki persamaan lingkaran, diperlukan penguasaan terlebih dahulu mengenai jarak dua titik. Dengan menggunakan Theorema Phytagoras, kita dapat menemukan jarak antara dua titik (d) yaitu dengan pemisalan titik A (x1,y1) dan B (x2,y2,) .
Dengan menggunakan definisi lingkaran dan mencari jarak antara dua titik tersebut, diharapkan siswa dapat menemukan rumus persamaan lingkaran dengan pusat O(0,0) dan jari – jarinya r.
C. Persamaan Lingkaran dengan Pusat O(0,0) dan jari–jari r
Untuk memudahkan penulisan rumus, kita dapat menghilangkan indeks 0 pada x0 dan y0, sebab maknanya akan sama saja. Sehingga akan menjadi .
Jadi , persamaan lingkaran dengan pusat O(0, 0) dan jari-jari r adalah :
x2 + y2 = r2
D. Persamaan Lingkaran dengan Pusat M(a,b) dan jari–jari r
Contoh Soal
E. Bentuk Umum Persamaan Lingkaran
Dengan menggunakan persamaan lingkaran dalam bentuk umum, siswa dapat menemukan pusat dan jari – jari lingkaran, dengan cara sebagai berikut :
Persamaan Lingkaran:
Contoh Soal
F. Kedudukan Titik Terhadap Lingkaran
Contoh 5
G. Kedudukan Garis Terhadap Lingkaran
Secara geometri ada tiga kedudukan garis terhadap lingkaran, yaitu :Contoh
Tentukan posisi garis y = 3x + 2 terhadap L x2 + y2 + 4x – y + 1 = 0 !
Jawab :
Subtitusi garis y = 3x + 2 ke L x2 + y2 + 4x – y + 1 = 0, diperoleh:
x2 + (3x + 2)2 + 4x – (3x + 2) + 1 = 0
10x2 + 13x + 3 = 0 sehingga nila a = 10, b = 13 dan c = 3
Nilai D = b2 – 4ac = 169 – 4.10.3 = 49 > 0
Karena diperoleh D > 0 maka garis y = 3x + 2 memotong ligkaran L di dua titik yang berlainan.
H. Jarak Titik Pada Lingkaran
1. Titik di luar lingkaran
2. Titik di dalam lingkaran
BAB III
PENUTUP
A. Kesimpulan
B. Saran
Perlunya trik khusus untuk menghafal berbagai rumus lingkaran yang dapat memudahkan siswa dalam mengerjakan berbagai macam soal yang berkaitan dengan materi lingkaran, selain itu juga perlunya latihan-latihan soal dari yang mudah hingga yang sukar.
KUMPULAN-KUMPULAN SOAL
PEMBAHASAN SOAL-SOAL